Use our P Value Calculator to compute values from Z, T, Chi-square, r, test statistic, mean & SD. Supports one-tailed & two-tailed p-value tests.
P-Value Calculator
P-value: A number (0 to 1) that tells how surprising your data are if the starting assumption (null hypothesis) is true. For example, flipping a fair coin 10 times and getting 8 heads has a p≈0.055. A small p-value (often below 0.05) means the result is rare by chance, suggesting the coin might be unfair. This guide explains P-values in plain English, with easy examples and a step-by-step calculator tutorial.
What Is a P-value?
Imagine you want to know if a trick coin is fair. You flip it many times and see some outcome. The P-value helps answer: How likely is it to get those results if nothing unusual is happening? In statistics, we start with a null hypothesis (e.g. “the coin is fair”). The p-value is the probability of getting the observed data (or something even more extreme) assuming the null hypothesis is true.
A P-value is between 0 and 1 – smaller values mean the result is more surprising. For instance, getting 8 heads out of 10 flips has a P≈0.055. That means there’s a 5.5% chance of 8 or more heads with a fair coin. If we set a “significance” level (often 0.05) ahead of time, then p≈0.055 is just above 0.05, so we’d say “the result could easily be by chance” and not reject the fair-coin idea. In short, a low p-value (like 0.01) suggests the result is too unusual under the null, so we reject the null hypothesis. A large p-value means the result is plausible by chance, so we do not reject the null.
Everyday Examples of Hypothesis Testing
Here are some simple stories to see P-values in action:
- Coin Tosses: Suppose you flip a coin 10 times and see 8 heads. Is the coin fair? Under the null hypothesis (fair coin, 50% heads), getting ≥8 heads is a binomial event. The probability of exactly 8, 9, or 10 heads is 0.044+0.010+0.001 = 0.055. This sum is the p-value. Because 0.055 is just above 0.05, you would “fail to reject” the fair-coin idea – it might be unlucky, but not impossible. If instead you saw 9 or 10 heads, the p-value would drop (smaller than 0.05) and you might suspect a biased coin.
- Dice Rolls: Roll a six-sided die 60 times. You expect about 10 sixes. Imagine you get 20 sixes. Is the die loaded? We set H0 = “die is fair (1/6 chance of six)”. The number of sixes follows a binomial (or approximately normal) distribution. We calculate how likely ≥20 sixes are under H0. If that probability (the p-value) is very small, we doubt the die is fair. Small tweaks in normal language: “A red die is shown, because rolling a die many times lets us count faces. We can compute a test statistic and p-value to judge fairness.”

- Medical Trials: Suppose a new medicine helped 30 out of 50 patients recover, while an old one helped 20 out of 50. Is the improvement due to the new drug or just chance? We test H0 = “no difference between drugs”. We compute a test statistic (like a Z or chi-square) from the two groups’ data, then find the p-value for that statistic. A small p-value (say 0.02) would mean “we’d only see such a big difference 2% of the time if both drugs were really the same.” In that case, researchers conclude the new medicine likely works better.
In each example, we start with a null hypothesis (coin fair, die fair, drug effect = 0) and calculate a statistic from data. The p-value translates that statistic into a probability under H0. Small p-values (e.g. 0.01 or 0.03) suggest “unlikely by chance” – so we reject H0. Large p-values (e.g. 0.2 or 0.4) suggest “quite possible by luck” – so we do not reject H0. Note this doesn’t prove H0 true; it just means the data don’t give strong evidence against it
Test Statistics (Z, T, Chi-square, F)
To compute a P-value, we first calculate a test statistic from our data. A test statistic is a number (often written as z, t, χ², F, etc.) that summarizes how far the data are from what the null hypothesis predicts. Different situations use different tests:
- Z-score (Standard Score): Measures how many standard deviations (σ) an observed value is from the mean under H0. The Z-test (or normal test) uses the standard normal distribution N(0,1). It’s best when you have a large sample size or know the population’s standard deviation. For example, comparing average heights between two very large groups. The formula is Z=(X−μ)/σZ = (X – \mu)/\sigmaZ=(X−μ)/σ, where X is your sample result, μ is the hypothesized mean, and σ the standard deviation.
- T-score (Student’s t): Like a Z-score but for small samples. Use it when you compare an average to a known value (or compare two small sample means) and the population variance is unknown. With more uncertainty in small samples, the t-distribution (which has fatter tails) is used instead of the normal. As sample size grows, the t-distribution approaches the normal. In practical terms, use a t-test for difference-of-means when your sample is “small” (often n<30).
- Chi-square (χ²): Used for categorical data, like counts in categories. Two common uses: (1) Testing a die or loaded coin (are observed face counts different from expected counts?). (2) Testing for independence in a contingency table (e.g. disease vs. treatment groups). The χ² statistic sums the squared difference between observed and expected counts (divided by expected). Only positive values make sense. A higher χ² means data are far from expected, giving a small p-value if too extreme.
- F-statistic: Used in ANOVA (analysis of variance). It’s a ratio of variances and tells us if the variability between groups is large compared to within groups. For example, comparing the average blood pressure across 3 different drugs: an F test can tell if at least one drug differs. Only positive values apply. Large F usually means a small p-value, suggesting group differences.
- Pearson’s r (Correlation): Sometimes listed here. It measures linear correlation between two variables (–1 to +1). You can compute a t-statistic from r (with df = n–2) to test if the correlation is significant. (But r is less common in basic “P-value for means” calculators.)
Each test uses a specific null distribution of the test statistic: Z and t have bell-shaped curves (normal or t-distribution), χ² and F have right-skewed curves. The degrees of freedom (explained next) help pick the exact shape. Once you know the test statistic value and distribution, you convert to a p-value (area in the tail(s) of the curve). See the table below for a summary:
| Test Statistic | When to Use | Example |
|---|---|---|
| Z (normal) | Large sample means or known variance. | Comparing average heights of two large groups (n=1000 each). |
| T (Student) | Small sample means, variance unknown. | Testing if a new teaching method changes average test score in class of 20 students. |
| Chi-square (χ²) | Categorical count data (goodness-of-fit or independence). | Checking if a die is fair based on face counts, or testing if gender (M/F) is independent of handedness (R/L). |
| F (ANOVA) | Compare variances or multiple means. | Comparing average weight loss among 3 different diets. |
These test names appear in many stats tools. For each, once you have the test statistic (z, t, χ², or F) and its degrees of freedom, you can find the corresponding P-value.
Degrees of Freedom
An important concept is degrees of freedom (df). This is roughly “how many values are free to vary” in your calculation. More precisely, it’s the number of independent pieces of information used to calculate the statistic. For example, estimating a population mean from a sample of size n imposes one restriction (the sample’s average), so df = n – 1 for a one-sample t-test. In a two-sample test, df often equals (n1 + n2 – 2).
Why does df matter? The shape of the t, χ², and F distributions depends on df. With more df (larger samples), the distributions become narrower (approaching the normal distribution). With very few df, the tails are heavier (more extreme values are likely). That’s why small samples use wider t-curves. Many calculators require you to enter df for the test statistic (e.g. “df = 9” for n=10 in a one-sample t-test). In practice, statistical software or online calculators will ask for the right df, so the correct p-value can be computed
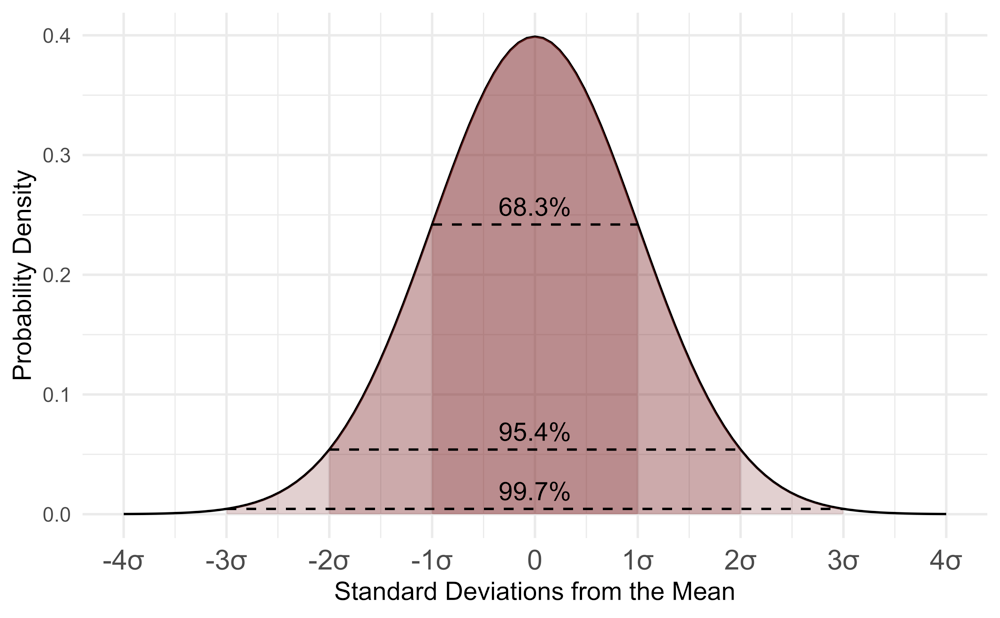
Figure: A standard normal (bell curve) with 1σ, 2σ, 3σ ranges marked (68.3%, 95.4%, 99.7%). A Z-score tells how many σ a result is from the mean. In P-value terms, a Z of ±1.96 (two-tailed) corresponds to p≈0.05.
Using a P-Value Calculator
Online P-value calculators let you quickly get a p-value from your test statistic. Here’s how to use one:
- Select the distribution: Tell the calculator which test you’re using (z-normal, t-distribution, chi-square, or F-distribution). This corresponds to your test statistic. For example, if you have a z-score, pick Normal; if t-score, pick t-Student; etc.
- Choose the tail type: Decide if your test is one-tailed or two-tailed.
- Two-tailed (most common): Tests for any difference in either direction (e.g. not equal).
- Right-tailed or left-tailed: Tests for a difference in a specific direction (e.g. “greater than” or “less than”).
Pick “two-tailed” if you only care that values are different (up or down). Use one-tailed if your hypothesis is directional (e.g. expecting higher or lower). The calculator will adjust the area (p-value) accordingly.
- Enter degrees of freedom (if needed): If you chose t or F, the calculator will ask for df. For a t-test with sample size n, df = n–1 (or n1+n2–2 for two samples). For F, there are numerator and denominator df. For a z-test, df isn’t needed.
- Input your test statistic: Type in your calculated statistic (z, t, χ², or F value).
- Set significance (optional): Many calculators default to α=0.05. This just sets a threshold for deciding significance. You can usually leave it at 0.05.
In short: pick the tail (two vs one), pick the distribution (Z, t, χ², F), enter any df, and enter your statistic. The calculator then shows the p-value and usually a decision (“reject H0” or “not significant”)
Interpreting Results
Once you have the p-value:
- Compare to α (significance level): Commonly α = 0.05. If p ≤ α, the result is called statistically significant. We reject the null hypothesis. If p > α, it’s not significant and we do not reject the null. For example, if p=0.03 and α=0.05, we say “p<0.05, reject H0”. If p=0.12, we say “p>0.05, no significant difference.”
- **Remember what p-value is: It’s not the probability that H0 is true, nor is it the chance your data were due to luck. It’s the chance of observing your data (or more extreme) assuming H0 is true. P-values are often misunderstood. Some mistakenly say “p=0.02 means a 2% chance the result is random,” but that’s not quite right. A p-value of 0.02 means “if H0 were true, there’s a 2% probability of seeing data this extreme.”
- Smaller is stronger: A p-value of 0.001 is stronger evidence against H0 than p=0.04. We can loosely say “the smaller the p, the more surprising the data under H0.” However, context matters (sample size, study design).
- Confidence vs significance: Sometimes people quote confidence intervals as more informative. But for beginners, remember: “Is p small or not?” is the core of the decision. Many tools also directly tell you “significant” vs “not significant.”
After using a calculator, it might say something like “Two-tailed p = 0.042; reject null (p < 0.05).” In plain terms, it means “There’s only a 4.2% chance of such a result if nothing was really different, so the result is statistically significant.”
Table of Common Tests (with Examples)
| Test | Use When… | Example |
|---|---|---|
| Z-test | Large sample or known variance; compare means or proportions. | Compare average height of two large random groups. Z= (mean₁–mean₂)/SE. |
| t-test (Student) | Small sample (n<30) or unknown variance; compare means. | Test if average test score of 15 students differs from 70%. t=(ȳ–70)/(s/√n) |
| Chi-square (χ²) | Categorical counts; goodness-of-fit or independence test. | Roll a die 60 times; test if counts match expectation. χ²=∑[(O–E)²/E] |
| F-test (ANOVA) | Compare means across ≥3 groups or variances ratio. | Compare average blood pressure for 3 diets (ANOVA). Large F ⇒ significant. |
| Correlation (r) | Measure linear association between 2 variables (n≥3). | See if study hours correlate with exam scores. Use t = r√[(n–2)/(1–r²)]. |
Each of these tests produces a statistic (z, t, χ², or F) and, if needed, an associated degrees of freedom. Then you find the p-value from the corresponding distribution.
Advanced Notes (for the Curious)
- P-values don’t measure effect size. A very tiny p could come from a trivial difference in a huge sample. Always consider how big the difference is, not just the p.
- P-hacking and misuse: Researchers caution against “chasing” p<0.05 by trying many tests. P-values can be manipulated by selective reporting. Also, an unexpected pattern in data might not get a low p even if it’s real, especially with small samples. So, design experiments well and report all analyses.
- “95%” myths: A common rule is “p<0.05 means 95% confidence.” But careful: a 95% confidence interval (CI) relatedly means that if you repeated the experiment many times, 95% of such CIs would contain the true value. Don’t confuse p-values with confidence probabilities of the hypothesis.
- One-tail cautions: Use one-tailed only if you really have a directional hypothesis and wouldn’t care about a result in the opposite direction at all. Often two-tailed is safer.
FAQs
A: It tells you how likely your data (or something more extreme) are if the null hypothesis is true. It’s the probability of the observed result under H0. It is not the probability that H0 itself is true. A smaller p means the result is more surprising under H0 (so we doubt H0).
A: The 0.05 threshold (5%) is a convention dating back to statistician Ronald Fisher. It means we are willing to accept a 5% chance of wrongly rejecting H0 when it’s true (Type I error). Many fields use 0.05, but sometimes 0.01 or other levels are used. The key is deciding your α level before testing. GraphPad notes that p-values are decimals between 0 and 1, “with some threshold (usually 0.05) deemed the significance critical value”
A: A two-tailed P-value checks for differences in either direction (higher or lower than expected). It doubles the tail area. A one-tailed P-value only looks at one side (e.g. “greater than” only). Two-tailed is more common unless you had a strong directional hypothesis. The calculator lets you pick tail type, which affects the computed p. For example, z=1.5 gives p≈0.067 two-tailed, but p≈0.067/2=0.033 one-tailed if you only cared about one direction.
A: Not “true,” but it means your data are quite consistent with the null. A large p-value means “no evidence to reject H0.” For example, in the coin toss above, p=0.055 was slightly above 0.05, so we fail to reject the fair-coin hypothesis – we can’t conclude bias from 8 heads in 10 flips. But this doesn’t prove the coin is fair; it just shows the result could easily happen by luck (5.5% chance)
A: It’s the number of independent pieces of info in the data after estimating parameters. In practice, for a t-test with one sample of n observations, df = n – 1. For ANOVA with two groups of sizes n₁,n₂, df = n₁+n₂–2, etc. More df means the test distribution is more like a normal curve; fewer df gives wider tails. Calculators ask for df so they know which exact curve to use
A: A very small p-value (like 0.001) means the observed result is extremely unlikely under the null hypothesis, which is strong evidence against H0. However, it doesn’t prove H0 is false with 100% certainty. Also, practical significance depends on context. But statistically, smaller p means stronger evidence – GraphPad notes “smaller is ‘better’ when it comes to interpreting P values for significance"
A: That’s on the usual cutoff. Some say “significant,” others say “right on the border.” It’s often better to say “p=0.050” explicitly. GraphPad’s wording is: if p is less than the critical value, reject H0. If p=0.05 exactly, you’re at the threshold – conventionally you might call it barely significant or just say p≥0.05 not significant. Always report the exact p-value and your chosen α.
A: P-values are a useful tool but have limitations. They can be misused (p-hacking) or misunderstood. A good experiment design and looking at effect sizes or confidence intervals is also important. But using a calculator correctly – and interpreting p-values as above – is a standard, reliable way to test hypotheses if you follow the rules.

